Moving water is a powerful entity responsible for lighting entire cities, even countries. Thousands of years ago the Greeks used water wheels, which picked up water in buckets around a wheel. The water’s weight caused the wheel to turn, converting kinetic energy into mechanical energy for grinding grain and pumping water.
In the 1800s, the water wheel was often used to power machines such as timber-cutting saws in European and American factories. More importantly, people realized that the force of water falling from a height would turn a turbine connected to a generator to produce electricity. Niagara Falls, a natural waterfall, powered the first hydroelectric plant in 1879.
Man-made waterfalls dams were constructed throughout the 1900s in order to maximize this source of energy. Aside from a plant for electricity production, a hydropower facility consists of a water reservoir enclosed by a dam whose gates can open or close depending on how much water is needed to produce a particular amount of electricity. Once electricity is produced it is transported along huge transmission lines to an electric utility company.
“By the 1940s, the best sites for large dams had been developed.” But like most other renewable sources of energy, hydropower could not compete with inexpensive fossil fuels at the time. “It wasn’t until the price of oil skyrocketed in the 1970s that people became interested in hydropower again.” Today one-fifth of global electricity is generated by falling water.
“Over the past 100 years, the United States has led the world in dam building. Secretary of the Interior Bruce Babbitt recently observed that ‘on average, we have constructed one dam every day since the signing of the Declaration of Independence.'” Of the 75,187 dams in the US, less than 3% are used to produce 10-12% of the nation’s electricity.
With over 2,000 facilities, the US is the second largest producer of hydropower worldwide, behind Canada. The dams that do not produce electricity are used for irrigation or flood control. Many people believe these pre-existing sites could contribute to the country’s power supply in a cost-effective manner if hydroelectric facilities were constructed.
There are several favorable features of hydropower. Anywhere rain falls, there will be rivers. If a particular section of river has the right terrain to form a reservoir, it may be suitable for dam construction. No fossil fuels are required to produce the electricity, and the earth’s hydrologic cycle naturally replenishes the “fuel” supply. Therefore, no pollution is released into the atmosphere, and no waste that requires special containment is produced.
Since “water is a naturally recurring domestic product and is not subject to the whims of foreign suppliers,” there is no worry of unstable prices, transportation issues, production strikes, or other national security issues.
The reservoir of water resulting from dam construction, which is essentially stored energy, can support fisheries and preserves, and provide various forms of water-based recreation for locals and tourists. Land owned by the hydroelectric company is often open to the public for hiking, hunting, and skiing. Therefore, “hydropower reservoirs contribute to local economies. A study of one medium-sized hydropower project in Wisconsin showed that the recreational value to residents and visitors exceeded $6.5 million annually.” Not to mention the economic stimulation provided by employment.
Hydroelectric power is also very efficient and inexpensive. “Modern hydro turbines can convert as much as 90% of the available energy into electricity. The best fossil fuel plants are only about 50% efficient. In the US, hydropower is produced for an average of 0.7 cents per kilowatt-hour (kWh). This is about one-third the cost of using fossil fuel or nuclear and one-sixth the cost of using natural gas,” as long as the costs for removing the dam and the silt it traps are not included. Efficiency could be further increased by refurbishing hydroelectric equipment. An improvement of only 1% would supply electricity to an additional 300,000 households.
In the US, 81% of the electricity produced by renewable sources comes from hydropower. “Worldwide, about 20% of all electricity is generated by hydropower.” Some regions depend on it more than others. For example, 75% of the electricity produced in New Zealand and over 99% of the electricity produced in Norway come from hydropower.
The use of hydropower “prevents the burning of 22 billion gallons of oil or 120 million tons of coal each year.” In other words, “the carbon emissions avoided by the nation’s hydroelectric industry are the equivalent of an additional 67 million passenger cars on the road 50 percent more than there are currently.” The advantages of hydropower are therefore convincing, but there are some serious drawbacks that are causing people to reconsider its overall benefit.
Since the most feasible sites for dams are in hilly or mountainous areas, the faults that often created the topography pose a great danger to the dams and therefore the land below them for thousands of years after they have become useless for generating power. In fact, dam failures do occur regularly due to these terrain conditions, and the effects are devastating.
When a new dam’s reservoir floods the countryside, people who live in the area have to move and relinquish their former lifestyles in order to make way for the project. This is very stressful and often controversial, especially if a community has maintained a particular way of life on the same land for generations.
Such is the case in Chile, where the indigenous Pehuenche “are currently fighting construction of the 570MW, US $500,000,000 Ralco Dam on the Biobo River Eight families continue to refuse to negotiate land exchanges with Endesa [the utility company], and wish to remain on their lands.”
If the project succeeds, a 13-square-mile reservoir would flood the land and force 600 people out of their homes, 400 of whom are Pehuenche “whose ancestral home is the upper Biobo.” A total of five dams have been planned, which “would force the relocation of 1,000 Pehuenches, 20% of the survivors of this ancient culture.”
The construction of a dam not only affects the people nearby, but it can also severely alter a river’s natural functions. According to American Rivers, a conservation organization, “by diverting water for power, dams remove water needed for healthy in-stream ecosystems. Stretches below dams are often completely de-watered.”
This may not seem like a significant problem until animal species are studied. Birds that have migrated to a specific riparian environment for generations no longer have enough insects on which to prey when the water level drops. If they have few migration alternatives, that could mean the endangerment of species that once flourished. Fish species such as salmon “depend on steady flows to flush them down river early in their life and guide them upstream years later to spawn. Stagnant reservoir pools disorient migrating fish and significantly increase the duration of their migration.”
Native populations of fish may decrease or disappear altogether due to temperature changes caused by dams. Slower water flow means warmer temperatures, and bottom-release of cold water means cooler temperatures. Several of hydropower’s disadvantages focus on fish. It is easy to forget how important fish and other aquatic life are, some of which reside at the bottom of the food chain.
The environmental changes caused by hydroelectric projects may be obvious to the local biologist but elude the average person. Most people will more readily notice a smoggy haze developing in an area where a coal plant is operating than a smaller population of a particular bird species where a hydropower facility functions. Such oversights lead people to believe that nothing is wrong.
Hydroelectric companies and organizations often emphasize their “clean” manufacture of electricity and neglect to mention the long-term environmental hazards. “Dams hold back silt, debris, and nutrients.” Silt collects behind the dam on the river bottom, accumulating heavy metals and other pollutants. Eventually, this renders the dam inoperable, leaving the mess for future generations, who will either have to remove the collected debris or live with a potentially catastrophic mudflow poised to inundate the area below the dam.
There is also a debate between preserving rivers for their aesthetic value versus meeting the energy needs of thousands of people. The latter has prevailed. Today “there are 600,000 river miles impounded behind dams. In contrast, only 10,000 river miles (not even half of 1%) are permanently protected under the National Wild and Scenic Rivers System.” The only undammed river in the US that is longer than 600 miles is the Yellowstone.
Hydropower may be better for the environment than fossil-fuel sources, but its future is so uncertain that we may need to focus on other alternatives. According to the National Hydropower Association, “an increasing array of statutes, regulations, agency policies and court decisions have made the hydroelectric licensing process costly, arbitrary and time-consuming.
A typical hydropower project takes 8 to 10 years to find its way through the licensing process. By comparison, a natural gas fired plant, which emits significant carbon dioxide (CO 2 ) gases, can typically be sited and licensed in 18 months. Given this uncertain climate, few investors are willing to risk their capital on new hydropower development. Furthermore, some project owners and operators contemplate abandonment of their projects rather than proceeding with relicensing.”
Relicensing is a complex process in which private dams are re-evaluated every 30 to 50 years. The Federal Energy Regulatory Committee “considers anew whether it is appropriate to commit the public’s river resources for private power generation FERC is now required, when deciding whether to issue a license, to consider not only the power generation potential of a river, but also to give equal consideration to energy conservation, protection of fish and wildlife, protection of recreational opportunities, and preservation of other aspects of environmental quality.”
Relicensing was infrequent until 1993, when hundreds of licenses began to expire. “The Hydropower Reform Coalition formed in 1992 to take advantage of this once-in-a-lifetime opportunity to restore river ecosystems through the relicensing process.” To the Coalition’s dismay, a new bill is being considered called the Hydroelectric Licensing Process Improvement Act, which if passed, “would limit the abilities of federal agencies to protect natural resources,” making relicensing easier for dam operators.
Some people favor dam removal so that healthy rivers and riverside communities can be restored, but American Rivers reports that most of the larger dams in the US “are not likely candidates for removal.” In that case, it may be wasteful not to use them to their full potential as long as they are still sturdy.
A hydropower assessment conducted by the US Department of Energy found that 4,087 sites could be developed without constructing a new dam. “The assessment consider[ed] such values as wild/scenic protection, threatened or endangered species, cultural values, and other non-power issues. If all of this potential were to be developed 22.7 million metric tons of carbon could be avoided.” But this savings in carbon emissions pales when compared to the tonnage of silt and other material that must be handled if the river is to be restored to a freely-flowing state. All rivers will eventually silt up the dam.
At this point, future generations will have the choice to either keep the useless dam or remove it. Keeping the poorly consolidated silt and mud behind the dam is potentially dangerous. Removal costs will often exceed the value of power produced over the dam’s lifetime.
Unlike other renewables such as wind and solar power that receive more praise than criticism, hydropower is a highly controversial issue. While it does have many merits, if we ignore the critics’ warnings, we may not realize its full impact on our natural resources until it is too late.
History of Hydropower
Water has been used for energy purposes for thousands of years. It has been used for motive energy in many parts of the world for at least two thousand years, primarily for grain milling. Water mills were constructed all over Europe and North America during the first decades of the Industrial Revolution to provide motive (shaft) power for a variety of uses, from flax processing to textile spinning and weaving, from timber milling to wood working.
All hydropower energy was produced from small hydro schemes (i.e., less than 10 MW) until the beginning of the 20th Century. In fact, almost all hydropower schemes until the late 19th Century were mini (less than 1 MW) or micro (less than 100 kW). Thousands of towns and cities in the world are located around these early small hydropower sites showing the heyday of hydropower in the 18th Century. Hydropower was eclipsed in the late-18th Century for nearly one hundred years by the discovery of coal. Coal quickly became the primary energy source for most of the 19th Century, and many hydropower sites were either abandoned or neglected.
However, hydropower witnessed another renaissance with the discovery of electricity in the latter part of the 19th Century. Hydropower was the first major source for generating electricity, until coal, oil, and later nuclear, became more prominent. Still, hydropower accounts for nearly 10% of the world’s commercial energy and accounts for over 90% of the electricity generated in such countries as Norway, Austria, and Kenya.
Initially, hydroelectric plants were small or micro-hydro sites. However, the industrial and domestic demands called for the construction of larger dams and hydropower schemes until small hydropower was once again in severe decline by the end of the first half of the 20th Century.
This decline was accelerated with the advent of cheap petroleum products in the post-World War II era. These two factors (large hydro and cheap petroleum) nearly spelled the end for small-scale hydropower by the 1950s. Thousands of small hydro-electric plants were abandoned in Europe, Asia, and North America from the 1950s to the early-1980s. Small hydropower plants virtually ceased to exist in the Former Soviet Union (FSU) and Central and Eastern Europe (CEE).
However, since 1989 there has been yet another renaissance of small hydropower in Europe. This has been particularly pronounced in CEE, as the economics of production have improved, and as concerns for reducing environmental emissions have increased. Since 1989 over 2000 small hydroelectric plants have been renovated in Europe, while another 1000 new plants have been constructed.
Resource Potential
About 680 GW of hydropower has been developed globally, 47 GW of which is small hydropower (<10 MW/site). The remaining non-utilized global hydropower potential is estimated at 3,000GW, 180 GW of which is at small hydro sites. 70% of this small hydro potential (126 GW) is in developing countries.
Table 2: Estimates of Small Hydro Capacity and Production by Region (1995)
| Region | Capacity (MWe) | Production (GWh) |
| North America | 4,400 | 18,000 |
| Latin America | 1,000 | 3,500 |
| Western Europe | 9,740 | 40,000 |
| CEE and FSU | 2,070 | 8,500 |
| Mid East and Mediterranean | 180 | 700 |
| Africa | 400 | 1,600 |
| Pacific | 160 | 700 |
| Asia | 10,000 | 42,000 |
| Total | 27,950 | 115,000 |
Sources: International Water Power and Dam Construction Handbook (1996) Hydropower and Dams: World Atlas (1997)
The World Energy Council estimates that, under current policies, installed capacity of small hydro will increase to 51 GW by 2020, with the largest increase coming in China. Under the WEC’s favorable case scenario, installed capacity increases to about 75 GW by 2020. All regions of the world are experiencing significant increases in small hydro capacity, with China again showing the largest increase.
Table 2: Estimated Deployment of Small Hydro by 2010 By Region
| Region | Capacity (MWe) | Production (GWh) |
| North America | 5,500 | 25,000 |
| Latin America | 3,000 | 10,000 |
| Western Europe | 12,600 | 50,000 |
| CEE and FSU | 7,000 | 28,000 |
| Mid East and Mediterranean | 400 | 1,700 |
| Africa | 700 | 3,000 |
| Pacific | 750 | 3,000 |
| Asia | 25,000 | 100,000 |
| Total | 54,950 | 220,700 |
Sources: International Water Power and Dam Construction Handbook (1996) Hydropower and Dams: World Atlas (1997)
Of the estimated 130 hydropower turbine manufacturers in 1995, over 100 produce turbines and machinery only for small hydropower plants. Production is concentrated in Europe, North America, and Japan, although there are important producers in China and India. Micro-hydro producers are found all over the world, and new advances in this small-scale technology show the vitality of the industry.
Technologies
Small hydropower technologies can range from simple and inexpensive to complicated and expensive.
They can be constructed on:
- Natural reservoirs (e.g., lakes with stream run-off
- “Run-of-the-river” or “run-of-stream” schemes
- Piped water schemes (for irrigation and/or drinking water)
- Canals (for irrigation and/or drinking water)
Run-of-river schemes tend to be the most expensive, as they involve the construction of weir to catch water from a fast-flowing stream or river. The water is then diverted down a shaft, or “penstock” into the turbine. The turbine turns a generator that, in turn, generates electricity. Conversely, the turbine can turn a shaft for simple mechanical power or a combination of mechanical and electric power generation. Canal systems tend to be less expensive, as access and some infrastructure are already in place.
Nonetheless, the system is relatively similar to that of run-of-river systems. Costs per kilowatt installed can vary widely, but, if all civil works must be constructed for a hydro-electric small hydro system, prices per kilowatt range between US$ 750 and US$ 4,000, and can be higher or lower depending upon difficulty of access, size of system, among other factors.
Micro (and even “pico”, for less than 10kW) and mini-hydropower systems are being built all over the world. Nepal has one of the most successful micro-hydropower programs in the world. Considerable assistance has been provided to setting up micro-hydropower systems for mechanical power, primarily using “cross-flow” low-head turbines, with assistance from the Swiss and UK development agencies. Since 1980, hundreds of such schemes have been built. Since the early 1990s, many of these systems have been converted to generate electricity. Similar success stories can be found in India, Sri Lanka, and Peru in the developing world. China has installed thousands of small hydropower systems since the 1960s.
The least expensive small hydro systems are those that utilize pipe systems, generally systems carrying drinking or irrigation water from mountainous areas. These systems are inexpensive because they merely require the placing of a turbine on the pipe. Turbines can be standard (Peltons, Francis, etc.) or they can even comprise a pump put into reverse flow (the cheapest option of all). Such systems are being developed rapidly all over Central and Eastern Europe where over 1 GW of such systems have been installed since 1991.
Off-Grid Applications
Small hydro offers a number of possibilities for off-grid applications, as has been demonstrated vividly in Nepal and other parts of the developing world. However, applications are, by definition, limited to sites or areas where there is water.
Construction and installation costs can be high, but maintenance is very low. Furthermore, small hydro schemes have very long lifetimes, as the thousands of systems rehabilitated over the past decade in Europe and North America amply demonstrate. New improvements in technology are widening the scope for small hydropower, particularly for mini-hydro, micro-hydro, and pico-hydro applications.
Producing Hydroelectric Power
Small scale hydroelectric generation development
Introduction: The desire to produce one’s own electrical energy has been the goal of many consumers. This comes from the hopes that people have to become independent of the commercially produced electrical power and the distribution grid. The benefits of this independence include the availability of electrical power during power outages of the commercial grid, potentially lower energy costs, and the knowledge that one is in control of their own electrical energy needs.
During the last 30 or 40 years, people have become more aware of the fragile nature of our environment and many forms of alternative energy have been suggested with some actually implemented. Many, or most, of the alternate energy production facilities are designed and built by huge international companies. These facilities are organized for a quick payback. of investment and generating profit. They are also built to reduce harmful emissions and protect the environment.
In recent years “Pico generators” are referred to the equipment that generates up to SkW of electrical power. This amount of energy is enough to power a large single family home, a small farm or small workshop, a small school or clinic. The equipment can be solar powered, wind or hydro powered there are some others.
Hydro-power has been used for thousands of years. The early Greeks used hydro power to grind wheat into power over 2000 years ago. Little changed in the use of hydro power for some 1800 years. It continued to be used to grind wheat and also to move water to irrigate fields and mill lumber.
The 18th and 19th century brought about the beginning of the industrial revolution and the discovery of electricity. With electricity came the electric light bulb, electric motors and other devices needing electric power. Hydroelectric power was developed and frequently used then for these devices because it supplied relatively stable and low cost power. Currently about 19% of the world’s energy production is by hydro-power, most by very large facilities.
Electrical considerations:
There are really no difficulties with the electrical system of a small scale hydroelectric power plant. The theory is very Well developed and has been utilized many times in many locations globally. The required equipment is readily available from many suppliers.
Hydroelectric generators are slow to respond to load changes. in a small facility that is a particular problem, both the voltage and the frequency can experience large fluctuations with changing loads and this has to be controlled – The current state of the electrical and electronic technology allows for control systems the can control the voltage and frequency with the use of resistor, capacitor and transistor circuitry.
These systems are fairly expensive. A better, less expensive, way to control voltage and frequency is to let the turbine/generator run at a constant load and speed by using some sort of variable load in conjunction with the system load.
This system can only be used if there is enough water available to run the generator continuously at a particular load level. Since a lot of water is available a series of electrical heater coils can be used as a load bank. The water can either be contained in a tank and further used as needed or the water can just be heated and released.
If a tank is used to contain the heated water a thermostatically controlled system can be developed to keep the heat coils active as needed. As the load requirement changes the number of active heat coils can be increased or reduced to keep the generator load constant.
Financial considerations:
A 5 kW power plant, running at 90% of the time, will annually produce about 39,060 kWh of electric power, at 15 cents/kWh that comes to almost $6000 per year. The installation cost of a small scale hydroelectric plant varies widely, on the order of $1500-$10,000 per kW.
Assuming a cost of $2500 per kW, total cost of $12,500 for a 5 kW plant, the payback on investment would be a little over two years. Consider a remote location, three miles from an available electrical grid that has water available for a S kW hydro-plant. The cost of installing a commercial power line also varies greatly, from $4000 to $10,000 per mile or more. In this instance, a hydroelectric generating facility is very cost effective.
Making your own Hydroelectric Power
Construction:
In order to start construction, the first thing that needs to be done is to determine the characteristics of the available water. The height of the water source and the available water flow need to be determined. Once that is done, the right equipment can be selected.
There are a huge number of equipment manufacturers and distributors available. Internet search engines make the selection process simple although time consuming. After the equipment, the stock pipe line, power house, and electrical system can be designed. Many variables exist in equipment and location so each facility will have its own, unique, set of parameters to consider.
In non-rural areas, there may be regulations prohibiting self-generation facilities.
Equipment selection:
Hydroelectric electricity needs a steady source of water. The power output of even a small power plant depends on both the pressure and volumetric flow of water. The higher the pressure the less water flow is needed, and inversely the lower the pressure the more water flow is required.
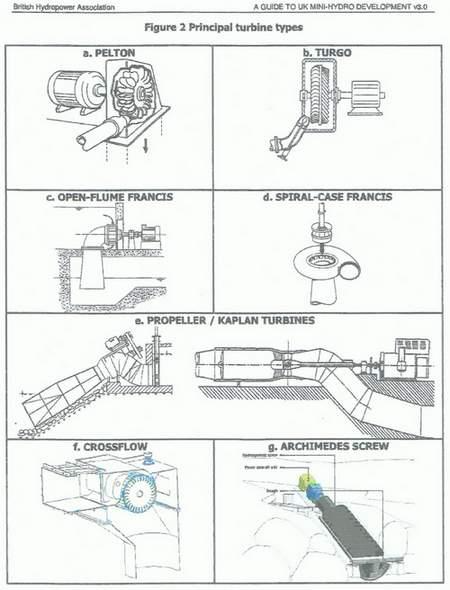
Hydro-power equipment is normally divided into three groups, high pressure, medium pressure and flow rates are low, medium and high. High pressure system include a pipe line (pen-stock) and usually a “Pelton” type wheel. A Pelton wheel is an impact driven device. A Pelton wheel has buckets which the high pressure water stream strikes causing it to rotate which turns the attached generator producing electricity.
Pelton wheels are normally used where the height of the water drop exceeds 70 meters. Pelton wheels are 80.90% efficient. A Pelton wheel turbine controls generator output by restricting water flow from a high pressure nozzle. Medium pressure hydroelectric generators use either Kaplan, Francis or Turgo turbines. Francis and Kaplan wheels are called reactive devices because they are driven by water passing over them.
These turbines are used from 10-70 meters water drop. They use what is called “wicket gates” to control the water entering the turbine. They are somewhere in the neighborhood of 90% efficient in converting the potential energy of the water to shaft rotational energy supplied to the generator.
Some of the equipment used for low pressure systems include a reverse Archimedes screw, a water wheel, or a bulb turbine set in a river. A paddle wheel in a river can produce significant electrical energy. These types of hydroelectric generators can produce energy for water drops well under 10 meters. Efficiencies range from 65% to 85%.
Water requirements:
Generally the higher the water drop (head pressure) is the lower the required water volume flow is for the same power output. The equation that can be used to model a hydroelectric plant can be expressed as P=9.8I*Q*h*E where P is the output power in kw; Q is the flow rate in cubic meters per second, h is the drop height in meters and E is the efficiency in percentage.
There are several other equations that are important.
Water velocity at the turbine can be calculated by V=sqrt(2*g*h)_, where g is the gravitational constant (9.81 meters! sec”?2) and h is again the height of the water drop in meters. Then the pen-stock pipe area is A=Q/V. From that equation, the diameter of the pen-stock pipe is D=sqrt(4″A/3.1415). These equations will now be used to model three hydroelectric projects, a high pressure system using a Pelton wheel, a medium pressure system with a Francis wheel and a low pressure system with a reverse Archimedes wheel. The assumptions for the high pressure system are that the desired output should be 514W and that the height of the water source is at lSO meters. The efficiency is conservatively set at 75%.
Calculating for the volume low rate, Q=5/(9.81 * l50*.75), gives .0045 cubic meters/sec, 4.5 liters/sec, 272 liters/minute. The water velocity at the turbine wheel is V=sqrt(2*9.8l*l50), gives 54 meters/second. The pipe area calculation gives A=.?)045f54, or D0008 square meters, pipe diameter is D=sqrt(4*.00008/3.1415), or .010 meters, 1 cm.
This 1 cm opening is the diameter of the power nozzle supplying high pressure water to the Pelton turbine wheel – A pen-stock pipe normally brings the water from the source so the power plant. Although only a 1 cm opening is theoretically required to produce the desired power it is not practical to run a pipe that size from the source. As the diameter of a pipe is reduced the water velocity increases, as the velocity increases so do the friction losses. In order to maintain the flow rate, the pen-stock diameter must be increased to reduce the friction losses.
To keep the friction losses below 10% the pen-stock diameter must be 7.5-10 cm. This is calculated to keep the water velocity in the pipe at .8-1.5 meters/second. Often, a designer will size the pen-stock in sections so that the upper third of the pipe is three times the diameter of the lower third and the middle third section is twice the diameter of the lower third. This is also done to reduce the pipe friction and improve water flow and efficiency.
For a medium pressure system a Francis wheel is considered, 5lrW output, water height is 40 meters, efficiency again at 75%. Calculating for ?ow rate Q=5/(9.81 *4O*.75) gives .01 7cubic meters/sec, l7 liters/sec, 1019 liters/min. Velocity at the turbine wheel is V==sqrt(2*9.81*4O) or 28 meters /sec. The pipe area calculation gives A=.0l7/28 or .0006 square meters and a pipe diameter of D= sqit(4*.0006/3.1415) or about 2.8 cm. As before this is the size of the opening leading to the Francis wheel. In order to reduce the velocity to .8 meters per second, in the pipe, to reduce friction losses the calculation is A=.Ol7/.8, then D=sqrt(4*A/3.1415) or 16.5 cm.
For a low pressure system, a reverse Archimedes wheel can be used to generate electrical power. The assumptions here are a 5kW output and a water height of 4 meters, efficiency 75%.
Flow rate is Q=5/(9.81 *4*.75) gives .17 cubic meters/sec, 10,000 liters/minute, water velocity at the turbine intake is 8.9 meters/sec and the pipe diameter calculates to 15.6 cm Because of the specifics of the Archimedes screw, it is an open pipe, and the requirements of a slow water velocity the size of the required pipe increases to 75-100 cm.
The potential power that can be generated from a water resource can always be determined from the equation P=9.81*Q*h*E, the variables, constants and units are as described above. For example, a water source at 80 meters with an available flow of .006 cubic meters/sec and an equipment efficiency of 80% could generate 3.5 kW.
For high and medium pressure facilities obstructions at the intake site is always a problem. Floating debris can get into the pipe causing major problems at the turbine. A small dam and pool can be built which allows the inlet to be at some level below the water surface allowing debris to float by the inlet. Metal gradings and screens can be fabricated to allow debris move past the inlet.
Power Grid Connections
For decades, many commercial energy producers and distributors have been required to pay for electrical power that is made available and pushed into the electrical distribution grid.
Extra power produced by small scale hydroelectric plants can be supplied back to the grid producing income. There are some safety devices required to make this sort of system workable. At a bare minimum, both a positive disconnect from the utility grid and a reverse power protection relay are required. Both of these are readily available. The positive disconnect is required to protect utility employees working during power outages and the reverse power relay protects the power plant equipment.
The additional advantage of connecting to an existing power grid is that there is then no need for any control of the voltage and frequency of the hydroelectric generator. The grid sets the voltage and frequency and the generator just supplies a constant load to the grid, making the control circuitry much simpler.
Hydropower as Renewable Energy
Hydropower has become “the leading source of renewable energy. It provides more than 97% of all electricity generated by renewable sources worldwide. Other sources including solar, geothermal, wind, and biomass account for less than 3% of renewable electricity production.”
Hydropower is very convenient because it can respond quickly to fluctuations in demand. A dam’s gates can be opened or closed on command, depending on daily use or gradual economic growth in the community. The production of hydroelectricity is often slowed in the nighttime when people use less energy. When a facility is functioning, no water is wasted or released in an altered state; it simply returns unharmed to continue the hydrologic cycle.




